Level 3 FSMQ: support with permutations and combinations
24 September 2025
Steven Walker, Maths Subject Advisor

Permutations and combinations form part of the enrichment content in the FSMQ, offering students a valuable opportunity to engage with mathematical modelling beyond the standard GCSE curriculum. Problems extend the GCSE work on listing strategies and probability, helping students progress to more abstract thinking.
This blog highlights some of the most frequent misconceptions students encounter, using examples from past exam papers to illustrate key points and clarify common errors. In addition to the questions set for the FSMQ, a good selection of questions can be found from legacy Statistics 1 (AS) modules for use in class.
Helping students distinguish between permutations and combinations
The most common misconception is incorrectly assuming that the terms permutations and combinations are interchangeable. Students need to remember that:
- Permutations are used when order matters.
- Combinations are used when order doesn’t matter.
Example
Question 1 2019 FSMQ – 6993

This is a permutation:
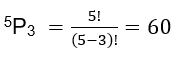
Simply choosing 3 three people from the committee of five people would be a combination:
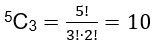
Quick tip for success: ‘Does order matter?’
Avoiding mistakes with repeated items
Students often forget to adjust for repeated items when calculating arrangements, leading to incorrect totals.
Example
Question 6(b) 2016 Probability & Statistics 1 – 4732

The correct count, remembering that the A appears three times and both the B and E appear twice giving
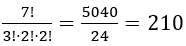
Common errors include ignoring repeated letters: using just 7! or only considering the number of distinct letters: using 3!.
Quick tip for success: ‘Are there repeated items?’
Spotting hidden constraints
Students sometimes apply formulas without considering the context or constraints given in the question.
Example
Question 3 2022 FSMQ – 6993

In this question, the captain must stand in a fixed position, and the vice-captain can only stand to the left or right of the captain. Therefore only 7 students need arranging (7!) multiplied by 2 for the vice captain to be positioned on either the left or right of the captain. Whilst many scored full marks on this question, some students overlooked these restrictions and applied a standard permutation formula without adjusting for the context.
Quick tip for success: ‘Look for constraints (fixed positions, limited choices).’
Breaking problems into manageable cases
Students may try to apply a single formula to a problem that requires breaking it into multiple cases.
Example
Question 6(a) 2016 Probability & Statistics 1 – 4732

Most candidates recognised that this involved the use of the combinations formula, but some students missed that the total number of objects changed at each step, leading to incorrect substitutions. The correct calculation should be
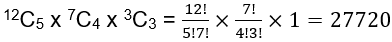
Quick tip for success: ‘Break complex problems into smaller parts.’
Final thoughts
Mastering permutations and combinations requires more than memorising formulas. Students should:
- Ask whether order matters
- Watch for repetition and constraints
- Break complex problems into cases when needed.
One way to help students engage with the context of the question is to encourage the use of diagrams to identify valid (and perhaps invalid) arrangements.
This topic helps students develop the skills to think critically about the structure of a problem and supports the progression from GCSE to A Level Maths.
Topic based exercises can be created using past paper questions held on ExamBuilder.
Stay connected
Sign up for our termly FSMQ teacher networks and professional development webinars.
If you have any questions, you can email us at maths@ocr.org.uk, call us on 01223 553998 or message us on X @OCR_Maths. You can also message me @stevemaths.bsky.social (personal account).
Sign up for subject updates to receive the latest maths news, updates and resources.
If you are considering teaching any of our qualifications, use our online form to let us know, so that we can help you with more information.
About the author
Steven originally studied engineering before completing a PGCE in secondary mathematics. He has taught secondary maths in England and overseas. Steven joined OCR in 2014 and worked on the redevelopment of OCR’s FSMQ and the A Level Mathematics suite of qualifications. Away from the office he enjoys cooking and to travel.
Related blogs by the same author