Problem solving in GCSE (9-1) Maths: examples of good practice
04 December 2023
Amy Dai, Maths Subject Advisor

Back in 2015 there was curiosity and uncertainty about the larger role problem solving would take in the new reformed GCSE (9-1) Maths. Darren Macey, OCR Subject Specialist in Mathematics, discussed this at the time in a series of blogs, The problem with problem solving part 1, part 2, and part 3.
In my first blog, I looked at the overall changes to the way in which problem solving is taught since the qualification reform. In this second blog, I look more closely at how problem solving has appeared in question papers, along with some examples of good student practice.
Looking at AO3 in more detail
In GCSE Maths (9-1), each assessment objective (AO) is broken down into more detailed assessment criteria.
AO3: Solve problems within mathematics and in other contexts, is broken down into:
- translate problems in mathematical or non-mathematical contexts into a process or a series of mathematical processes
- make and use connections between different parts of mathematics
- interpret results in the context of the given problem
- evaluate methods used and results obtained
- evaluate solutions to identify how they may have been affected by assumptions made.
AO3 makes up 30% of the marks in the Higher tier papers, and 25% of the marks in the Foundation tier papers. For more information on the different AOs and how they show up in the exam papers, please take a look at our Exploring our question papers resource.
Problem solving in exam questions
Here are some examples of past exam questions that are targeted towards AO3.
Example 1
This list represents four numbers.
127 x x+1 2x
The mean of the four numbers is 180.
Work out the numbers.
You must show your working.
[5]
J560/01, June 2022
This question targets both AO1 and AO3. It requires students to ‘make and use connections between different parts of mathematics’ as they must combine their knowledge of the mean with their knowledge of algebra. It also requires them to ‘translate problems in a mathematical context into a process’.
Example 2
In January 2018, an art collector bought an antique painting.
In January 2020, he sold it for £17 640.
Assume the value of the painting increased by 5% each year.
Calculate the art collector’s profit.
You must show your working.
[5]
J560/04, June 2022
This question also targets AO1 and AO3. The question is set within a real-life context, requiring students to ‘translate the problem from a non-mathematical context into a series of processes’. To gain the final method mark, the student must demonstrate their problem solving skills to link what they have worked out (the value of the painting in 2018) with the amount of profit gained by the art collector.
Examples of good practice
Here are some examples of candidate responses to the above questions to illustrate how AO3 can be demonstrated successfully by students.
Example 1
This list represents four numbers.
127 x x+1 2x
The mean of the four numbers is 180.
Work out the numbers.
You must show your working.
[5]
J560/01, June 2022

This candidate response scored 4 out of the 5 available marks. They were able to gain full method marks by showing clear logical steps in their working along with evidence of working for each step. They have successfully linked their knowledge of the mean with simplifying and solving an algebraic equation. A good habit for students to develop is to write out prompts along their working, such as ‘all have to add to 720’, as it helps them to check their answers at the end. This candidate has taken the extra step of working backwards to check their answer (as shown in the bubble) which is also good practice.
Example 2
In January 2018, an art collector bought an antique painting.
In January 2020, he sold it for £17 640.
Assume the value of the painting increased by 5% each year.
Calculate the art collector’s profit.
You must show your working.
[5]
J560/04, June 2022
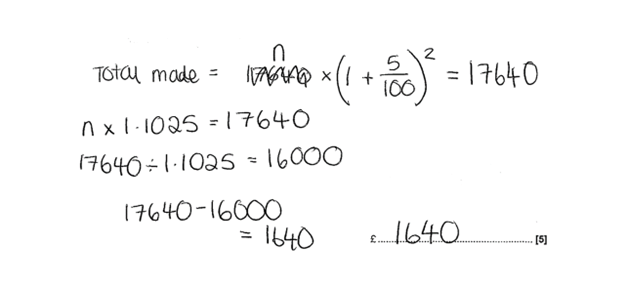
This candidate scored all 5 marks for this response. They were able to correctly translate the worded context into the correct process – recognising that this was a reverse percentages question. This was helped by a clear first line of working where the focus was on translating the percentage increase described in the question by use of the variable n as the unknown. This is another good example of a candidate setting their working out in a clear and logical manner.
Our support
Our Exploring our question papers resource not only illustrates how the different assessment objectives are assessed in our questions papers, it also outlines our accessibility principles and command words.
You can use our test-building platform, ExamBuilder, to find more examples of questions targeting AO3. In test creation it is possible to filter on assessment objectives to select questions that assess specific assessment objectives. This enables you to produce customised tests and mark schemes containing problem solving questions on any topic quickly and easily. For help in accessing ExamBuilder or tips on creating, saving, sharing and exporting tests, please refer to our ExamBuilder FAQs.
For examples of good exam question responses to problem solving questions, you can access candidate exemplars for all GCSE (9-1) Maths papers on our secure teacher website, Teach Cambridge (login required).
To learn more about student performance in problem solving questions, browse our professional development courses or sign up for upcoming GCSE (9-1) Maths network events.
Stay connected
Share your thoughts in the comments below. If you have any questions, you can email us at maths@ocr.org.uk, call us on 01223 553998 or tweet us @OCR_Maths. You can also sign up for monthly email updates to receive information about resources and support.
About the author
Amy joined OCR in 2023 after teaching for five years in both state and independent schools. She provides support across all the OCR Maths qualifications, but with a focus on GCSE, A Level Maths and Further Maths. She graduated from the University of York with a degree in Mathematics and Economics before gaining a PGCE in Secondary Mathematics and an MA in Education.
By the same author