A Level Mathematics - Why is standard deviation not standard across subjects?
06 October 2020
Hints and Tips - 7 minute read
 Steven Walker, OCR Maths Subject Advisor
Steven Walker, OCR Maths Subject Advisor
Mathematics is rightly defined as a facilitating subject; the skills learnt can be applied across the curriculum. Unfortunately the maths studied in the maths classroom does not always appear in the same form in other subjects. In this blog I will look at the support available for different subjects covering the topic of standard deviation in different ways.
Misconceptions
Students are often confused about why they may see ‘n’ or ‘n – 1’ in different formulae for standard deviation as they move between classrooms or in various textbooks.
It is not that one formula is better or more accurate (or even wrong), it is because the parameters used are different and the calculations are not measuring the same thing.
It is true that a large value for ‘n’ reduces the difference between the values calculated, but that does not mean that these formulae are equivalent when ‘n’ is large.
The formulae measure different things
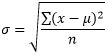
|
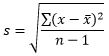 |
| This is the standard deviation of a set of data with size n. This might be the population standard deviation if we have all the data, or it is the standard deviation of the sample. |
This is an estimator of population standard deviation when investigating a population using a random sample from that population. |
Mathematics A – H230/H240
Psychology – H167/H567 |
Mathematics B (MEI) – H630/H640
Biology A – H020/H420
Biology B (Advanced Biology) – H022/H422
Geography – H081/H481 |
| Different qualifications have taken a specific approach and there is no requirement for students to make their own choice of appropriate formula in the examination room. |
Both these formulae can be written in a number of equivalent ways, but they are not equivalent to each other.
If you are investigating a set of data, then division by ‘n’ is correct if you are calculating the population standard deviation or the standard deviation of that sample.
However if you are using a sample in order to estimate properties of the whole population, then this calculation may be biased. The alternate formulae (dividing by ‘n – 1’) assumes that the sample has been taken at random from a normally distributed population and helps to correct for bias if you are interested in making some inference about the population from that sample.
Why ‘n – 1’?
Bessel’s correction is the use of ‘n – 1’ instead of ‘n’. It gives an unbiased estimator of the population variance, where the population is assumed to be normally distributed about the mean and that any errors in determining the mean and variance are independent. Since the sum of each of the sample values minus the sample mean must equal zero then there is one less degree of freedom.
Other correction factors may actually be appropriate depending upon the assumptions made about the underlying type of distribution of the population (but ‘n – 1’ is a useful rule of thumb correction to make).
The different approaches in A Level Maths
The DfE Mathematics AS and A level content April 2016 did not require anything beyond simply being able to calculate standard deviation.
In Mathematics A H230/H240 the formula for standard deviation has been used and there is no mention of estimators until Further Mathematics A H235/H245 where bias is introduced informally.
In Mathematics B (MEI) H630/H640 the assumption was that you will be more interested in what you can infer about the population from a sample and that this informal use of estimators was more appropriate here. Whilst every intention is for the context of any questions to follow naturally to the correct approach taken in the specification, there is no requirement for A Level Maths candidates students to consider when each formulae is the more relevant to the context.
Developing a deeper understanding
For most A Level students it is sufficient to recognise that there are underlying modelling assumptions that may limit the conclusions that can be drawn from the calculation.
Students taking Further Maths may well investigate biased and unbiased estimators of population variance, as well as the central limit theorem if they are taking a statistics option.
A full study of estimators may not be covered until higher education, either on a specific statistics degree or as part of a module on data analysis or experimental methodology.
Supporting your students
Always refer to the formulae quoted. Marks may be lost if the incorrect formulae is used (although it is true that as ‘n’ increases the difference between these two results becomes less significant).
OCR have produced a number of subject specific maths skills guides to support teachers and students.
Stay connected
What mathematical concept do you find is taught in different ways across the curriculum? Let us know via the comments below, or you can email us at maths@ocr.org.uk, call us on 01223 553998 or Tweet us @OCR_Maths. You can also sign up for email updates to receive information about resources and support.
About the author
Steven Walker, OCR Maths Subject Advisor
Steven joined OCR in 2014 and has worked on the redevelopment of OCR’s Entry Level, GCSE (9-1), FSMQ and A Level Mathematics/Further Maths qualifications. He now focuses mainly on supporting the Level 3 qualifications. Steven originally studied engineering before completing a PGCE in secondary mathematics. He began his teaching career with VSO in Malawi and has taught maths in both the UK and overseas.
By the same author