Studying A Level Further Mathematics at home
18 January 2021
Hints and tips - 9 minute read
 Steven Walker, OCR Maths Subject Advisor
Steven Walker, OCR Maths Subject Advisor
Important update
This blog was originally published on 12 May 2020
With schools entering a second ‘lockdown’ period, teachers and students may also be interested in a range of support videos that have been collated for each of the specifications of Further Maths by the Advance Maths Support Programme (AMSP).
Support videos
OCR was not involved in the production of these videos and whilst we feel they would be a useful resource, they do not form part of our endorsed support package.
Specifications are updated over time, which means there may be contradictions between the content coverage and the specification. Please refer to the information on the latest specification at all times.
AS Level and A Level Further Mathematics A – H235/H245
AS/A Level Further Maths A H235/H245 pure section Y531 and Y540/Y541
A Level Further Maths A H245 pure section Y540/Y541
AS/A Level Further Maths A H235/H245 Mechanics option Y533/Y543
A Level Further Maths A H245 Mechanics option Y543
AS/A Level Further Maths A H235/H245 Discrete option Y534/Y544
A Level Further Maths A H245 Discrete option Y544
AS Level and A Level Further Mathematics B (MEI) – H635/H645
AS/A Level Further Maths B (MEI) H635/H645. Core Maths Y410/Y420
A Level Further Maths B (MEI) H645. Core Maths Y420
AS/A Level Further Maths B (MEI) H635/H645. Statistics Y412/Y422/Y432
AS/A Level Further Maths B (MEI) H635/H645. Modelling with Algorithms Y413/Y433
AS/A Level Further Maths B (MEI) H635/H645. Numerical Methods Y414/Y434
A Level Further Maths B (MEI) H645. Further Pure with Technology Y436
A Level Further Maths resources
Continuing my series of blogs about studying maths qualifications away from the classroom, I now turn my attention to sharing resources I’ve sourced that are suitable for students studying, or thinking of studying, our A Level Further Maths.
Using the specification
All A Level Further Maths specifications have 50% of the content defined by the DfE, with the other 50% determined by the awarding body. We offer two specifications, which take slightly different approaches.
OCR AS Level and A Level Further Mathematics A - H235/H245
OCR AS Level and A Level Further Mathematics B (MEI) - H635/H645
As with A Level Maths, the majority of A Level Further Maths questions and resources can be used for practice purposes, irrespective of the specification you are following. Due to the slight differences in content however, it is important to check the notation and depth of topic coverage in your chosen specification.
Our maths support
We have published many free teaching resources that you can download for each of our A Level qualifications; just select your qualification from our maths web page.
Then select ‘Planning and teaching’ from the menu on the left to access the following resources:
- Delivery guides, which contain teaching notes and guidance on common misconceptions and mistakes along with a variety of links to both OCR and third-party resources.
- Section check-in tests, which have procedural, reasoning and problem-solving questions covering each of the sections of the specification.
Selecting ‘Assessment’ from the left-hand menu takes you to:
- Past papers and mark schemes for AS Further Maths from 2018, as well as question papers and mark schemes from the withdrawn legacy qualifications.
- Examiner reports for these papers, which detail the common mistakes and misconceptions seen by the marking team.
- Sample papers, which were written as part of the accreditation process, but have never been sat by students under exam conditions - as such the mark schemes may not have as much information as mark schemes for a live examination series.
- Links to the practice papers that are on the secure Interchange site - teachers will need a password to login and download these, which your Exams Officer will be able to help you with.
You can also find answers to frequently asked questions (FAQs) for each specification.
Learning without a textbook
Students may have access to an electronic copy of their class textbook, but don’t panic if not, there is a wealth of good quality maths support online.
You may find sites such as AMSP (formally Further Maths Support Programme), CAIE, Mathscentre, CIMT, Khan Academy, Maths Made Easy and Revision Maths useful and there are plenty more sources of notes, questions and demonstrations listed in our delivery guides.
It’s worth noting that candidates are never penalised for using alternative or more advanced techniques, unless the wording of the question specifically asks for a certain technique to be used. Remember also that if the specification uses a specific notation, then this is the notation that will be used in the examination question.
If you find you are struggling with a particular Further Maths topic, it may be worth referring back to the fundamentals that you covered in A Level Maths, or even from your GCSE course.
For greater challenge of the precursory A Level Maths content, you may wish to take a look at the Sixth Term Examination Paper (STEP). Focus on paper 1 in the first instance and remember to refer to their specification for the slight content differences between your A Level Maths course and the STEP content.
Their paper 2 approximately covers AS Further Maths content and paper 3 the full A Level Further Maths.
Use of technology
It’s worth mention here that the ‘use of technology’ is specifically referenced in the DfE criteria for A Level Further Maths (further details are provided in our specifications).
Some students may be without a calculator at home and whilst basic scientific calculators are available on most mobile phones, the free graphing and calculator apps that are available from platforms like Desmos and Geogebra (other providers are available) will be more useful for Further Maths.
In addition to functionality that can be used in the exam, students may want to make use of a computer algebra system (CAS) to check work or develop deeper conceptual understanding. There are free online platforms that can be used, such as WolframAlpha, Solumaths and Symbolab (others are available, some of which need to be downloaded).
These platforms also crucially have a vast wealth of prepared tasks and notes covering the breadth of content for A Level Maths and Further Maths specifications (and beyond). Used in conjunction with the specification, textbook and section check-in tests these are useful interactive tools for developing a deep understanding of the content, plus they’re also helpful for checking answers.
To illustrate, I have created the following Hyperbolic graph in Desmos, which can easily be shared.
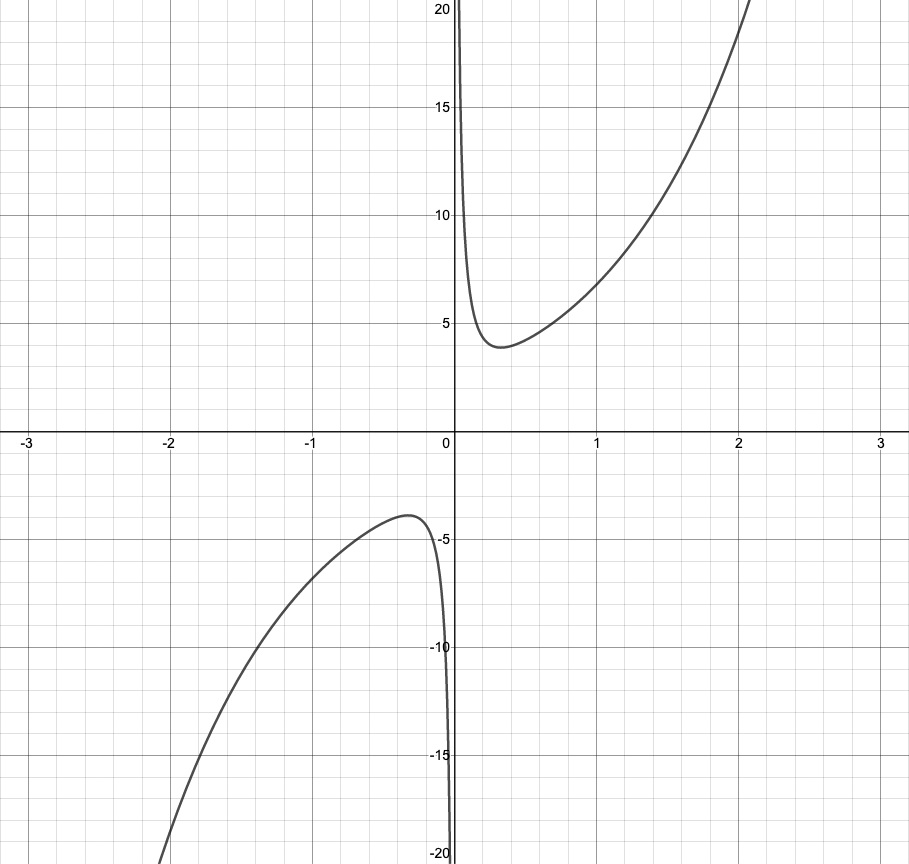
The question to ask your students is: what could be the equation in terms of Sinh and Cosh that created this curve?
For extra support in using your examination calculator, there are a wealth of tutorials and resources available online from Casio and Texas Instruments, plus many more on YouTube for almost all calculators, just search the model and function to find examples.
Mandatory pure content
There are many sources of independent learning material for the fixed pure content, though the standard caveat that there will be slight differences in approach applies (especially with regard to whether the content has been defined as AS or A Level).
As a starting point you may find the following useful:
- Mathematical induction from Richland Community College is quite a useful introduction to both proof and series.
- Chapter 3, complex numbers on the CIMT mathematics enhancement programme website gives a good overview of this topic.
- Section 9.3 of CIMT’s matrices and transformations covers the common confusion between an invariant line and a line of invariant points.
- An introduction to vector equations of straight lines from Paul’s Online Notes provides some initial notes and questions (with solutions).
- A basic introduction to roots of polynomials can be found on the Maths is Fun website.
- Mathcentre website provides a nice introduction to hyperbolic functions.
- Volumes of rotation features in the calculus content of Further Maths and a nice introduction to the disk integration method can be found on the Interactive Mathematics site.
- An introduction to polar coordinates can be found from NRICH, who also have puzzles such as the Maltese Cross to investigate the properties of differential equations.
- Mathcentre covers the content of differential equations for both Maths and Further Maths.
Optional content
One of the features of our Further Maths specifications is the opportunity to study extra options, with the final grade optimised based on students' performance in the examinations.
Traditionally there have been a significant number of candidates that will study an extra option independently; there may perhaps be more online support available for students of Further Maths because of this established study route. A great place to start is the AMSP.
The mechanics in action resource from Cambridge University Press can be downloaded from the STEM Learning site. This has a range of activities to help students overcome common misconceptions of the Mechanics topics in Maths and Further Maths (free registration needed).
Whilst the Further Statistics course does not include a large data set (LDS) requirement, students following the Maths and Further Maths courses in parallel may benefit from using the A Level Maths LDS to practice all their statistical techniques.
There is a nice introduction to graph theory in the Open Introduction on-line textbook for discrete mathematics from UNC for the Discrete (in OCR A) and Modelling With Algorithms (in OCR B (MEI)) options. This book also covers the arrangement and selection content of the Mathematical Preliminaries covered in the OCR A specification.
For those studying Additional/Extra Pure, or just as an interesting application of groups, this article on the mathematics of the Rubik’s Cube covers Lagrange’s Theorem.
Numerical Methods is an option unique to OCR B (MEI) Further Maths. Practise using numerical techniques on functions that you have worked out using other techniques in order to reinforce your understanding.
Similarly, the Further Pure with Technology option, again unique to OCR B (MEI), allows for investigation of material from the mandatory pure content using the skills required for this option.
Short activities and puzzles
We’ve been publishing puzzles via the @OCR_Maths Twitter account (search the #OCRMathsPuzzle hashtag), most of which are roughly around the GCSE level of demand. For A Level, they can be used to revisit the fundamentals, but they can also be used as starting points for further mathematical generalisation.
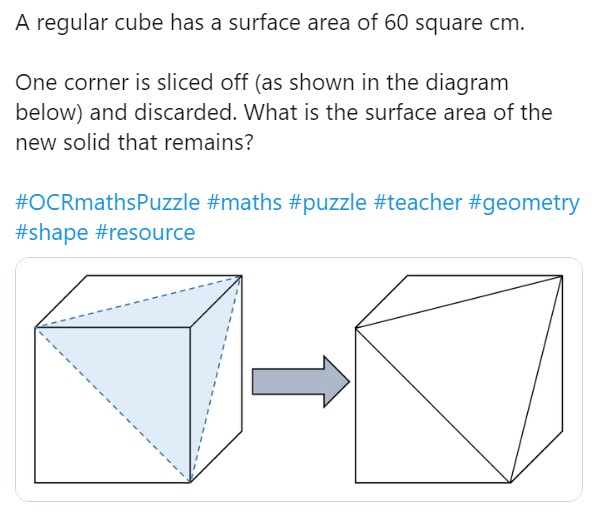
@OCRMathspuzzle 20 Sept 2019
This puzzle nicely reviews GCSE mensuration content on cubes and pyramids, but how about finding the vector equations for the planes?
Other sites with great short puzzles and activities include NRICH, Underground Maths, Risps, MSV, TES and many more.
We’ll also be regularly posting links to a variety of online resources in the coming weeks, so do follow us @OCR_Maths.
Stay connected
There are so many great online resources available, so join the conversation by sharing your ideas and links to all your favourites in the comment box below.
Look out for future blogs focused on the different options available for Further Maths.
If you have any queries or questions, you can email us at maths@ocr.org.uk, call us on 01223 553998 or Tweet us @OCR_Maths. You can also sign up to subject updates to receive information about resources and support.
About the author
Steven Walker, OCR Maths Subject Advisor
Steven joined OCR in 2014 and has worked on the redevelopment of OCR’s Entry Level, GCSE (9-1), FSMQ and A Level Mathematics qualifications. He now focuses mainly on supporting the Level 3 qualifications. Steven originally studied engineering before completing a PGCE in secondary mathematics. He is currently balancing his ‘work from home’ commitments with supporting his young daughter with reception year activities.
By the same author