Ten years of #OCRMathsPuzzle
12 July 2024
Steven Walker, Maths Subject Advisor

One of the important things the maths team is always happy to do is listen to your feedback about qualifications, so we can then support you in a variety of different ways. Back in 2014 the GCSE (9-1) Mathematics qualifications were getting accredited and one of the key aspects noted by teachers was the greater assessment of problem solving.
One of our responses was to start publishing a weekly #OCRMathsPuzzle, each Friday lunchtime during term time through our @OCR_Maths X channel (formerly Twitter). These help to support teachers by providing them with problems to use. The puzzles could be used regularly, either at the start or end of a lesson, during the following week or saved up to use at an appropriate time to enrich the teaching of specific topics. Over time we’ve gone on to post ones supporting a wider range of qualifications too, including Core Maths and A Level Maths.
The problem with problem solving resources
Unfortunately, problem solving has proven to be difficult to include in resources. Many resources we’ve seen signpost the route to a solution due to the questions being featured in a worksheet on a particular specified topic, or in a chapter on particular content.
Each #OCRMathsPuzzle is independent to any scheme of work so students would not have any implied starting point to the solution. The use of hashtags provides some hints if needed, but also signposts the themes and topics so that teachers can easily search through the puzzles for ones to use in class.
Not just exam questions
Examiners design questions that differentiate by task and have a distinct answer. Some of our puzzles are just alternate versions of exam questions. However, some are set to differentiate by outcome and some allow multiple valid answers. Our puzzles can use slightly more open language, which allows different students to go off on completely different trajectories. Students can discuss different approaches, give each other hints or make use of manipulatives and technology.
You can browse all of the past puzzles through the hashtag #OCRMathsPuzzle, but a few of our highlights are below!
#OCRMathsPuzzle
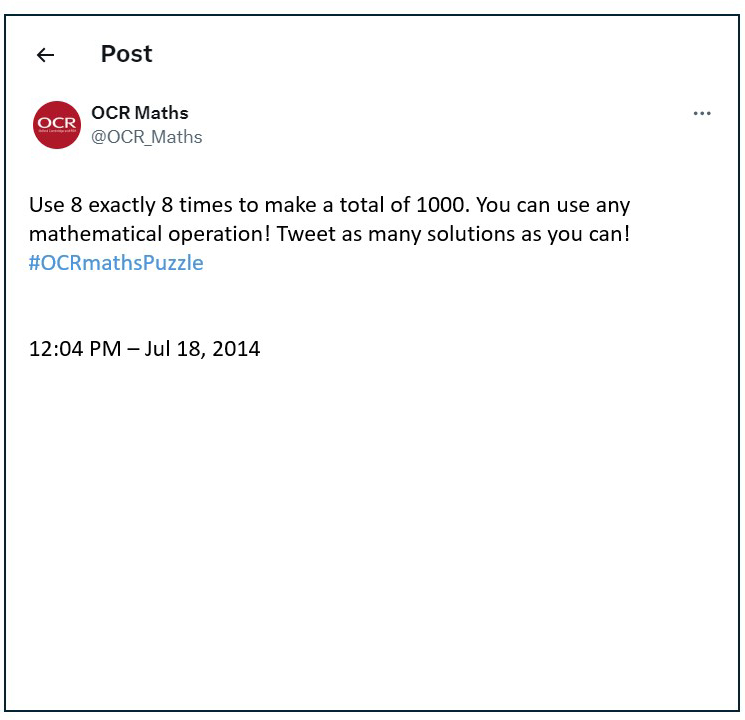
This was our very first puzzle, back in July 2014. This style of puzzle is very open ended with multiple solutions. Every attempt needs to be calculated and every incorrect solution is a learning opportunity.
#arithmetic
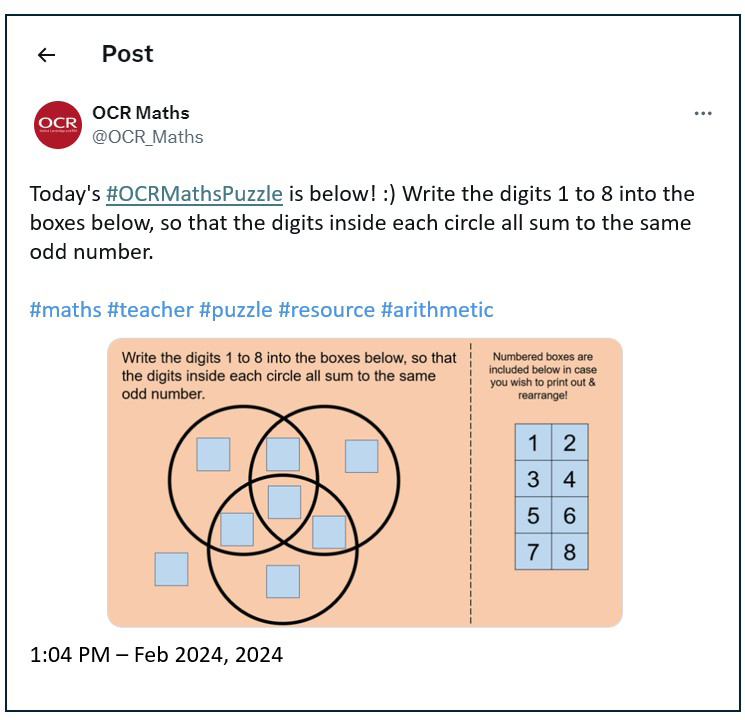
This puzzle specifically requested an odd total, to encourage students to think of the underlying mathematical properties, instead of permitting both evens and odds that would have probably in many cases led to just trial and improvement.
#algebra
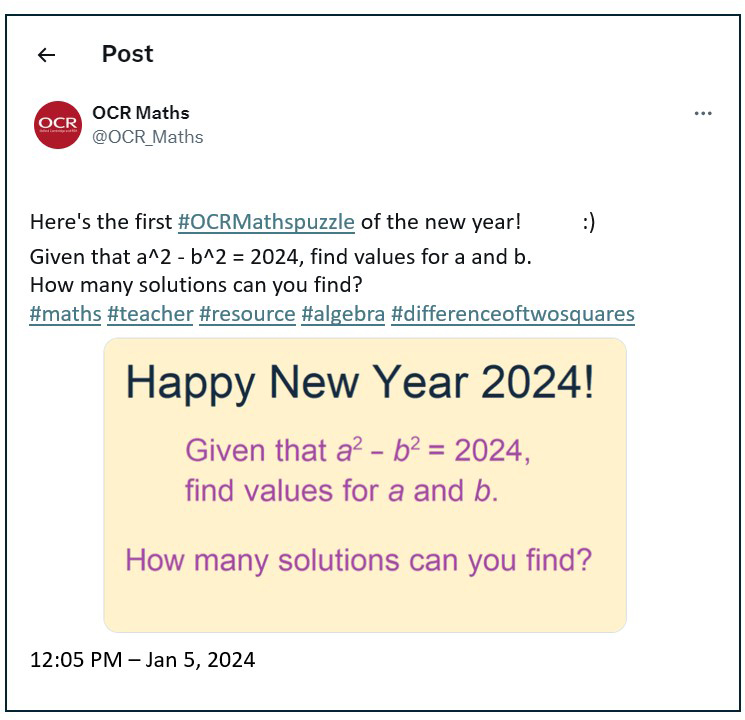
This New Year themed puzzle can be solved using the difference of two squares and prime factor decomposition to create pairs of simultaneous equations. Many readers assumed a and b could only be integers (and the puzzle could be adapted to request integer solutions from students), but one submitted solution was the continuous relationship between the variables.
#geometry
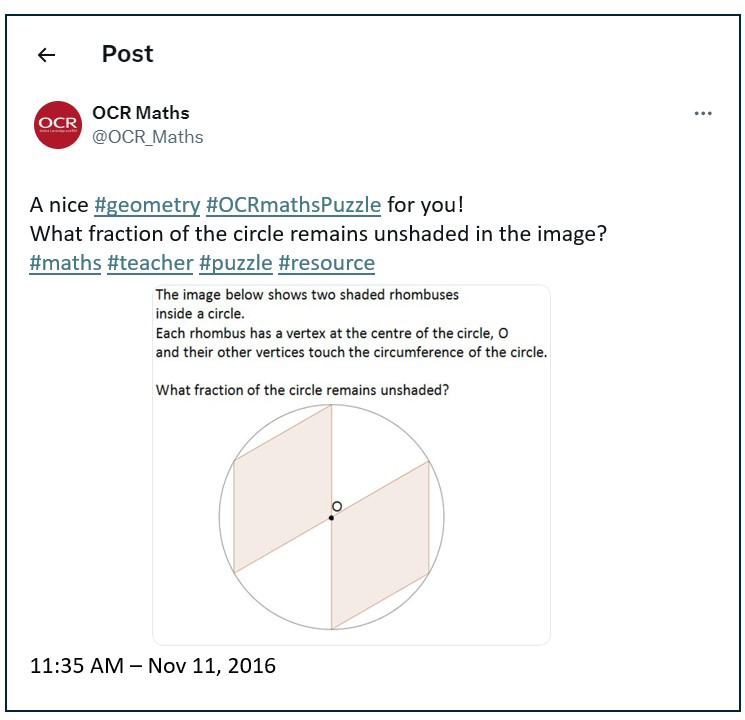
The key to solving many geometry puzzles set in circles is often to add in lines such as tangents or, as in this example, radii.
#technology
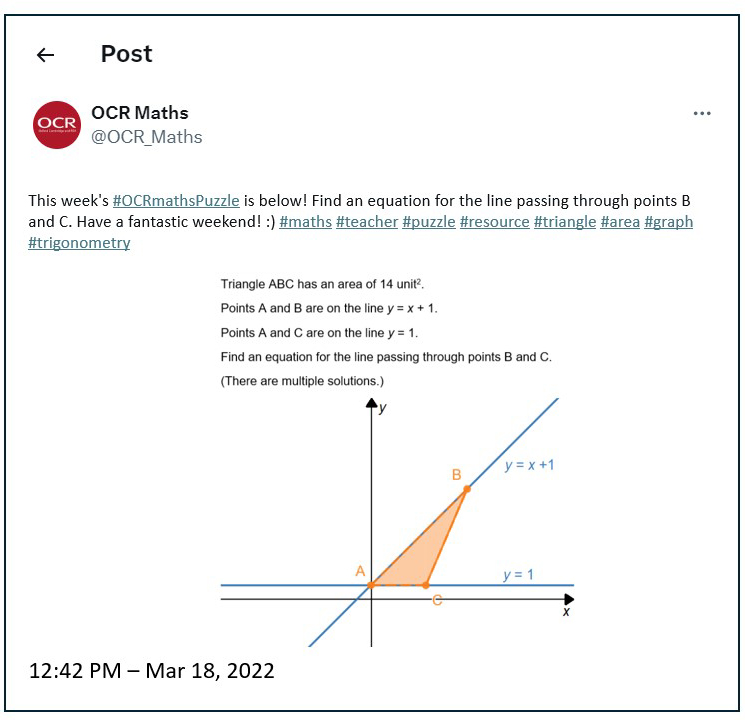
Many of the puzzles could be redrawn using dynamic graphing or geometric technology to adapt them as needed for students. For example, to extend this puzzle further, challenge students to set it up as a set of inequalities to shade the required region with the stated area. For example, see this Desmos graph version.
#area

Good problems can be created by linking geometric properties with algebra. Using the radius as a unit of measurement means students can calculate the side lengths and hence the area of each square. An additional challenge would be to request exact values in surd form or requesting the answer as a fraction or ratio.
#enrichment
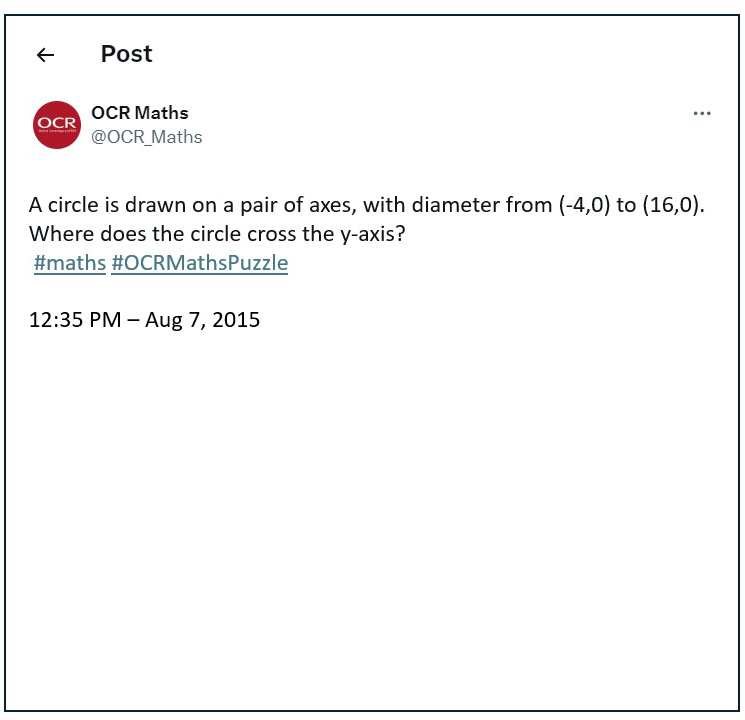
Initially, this puzzle appears to be an FSMQ or AS/A Level problem that requires finding the equation of the circle. However, using a sketch, the circle’s centre and radius can be found using GCSE knowledge. Pythagoras’ theorem can then be used to determine the two points where the circle will cross the y-axis.
Stay connected
What’s your favourite maths puzzle, or source of puzzles? Share a link in the comment box below.
If you have any queries, you can email us at maths@ocr.org.uk, call us on 01223 553998 or message us on X (formerly Twitter) @OCR_Maths. You can also sign up to subject updates and receive information about resources and support.
About the author
Steven originally studied engineering before completing a PGCE in secondary mathematics. He has taught secondary maths in England and overseas. Steven joined OCR in 2014 and worked on the redevelopment of OCR’s FSMQ and the A Level Mathematics suite of qualifications. Steven normally drafts the weekly #OCRMathsPuzzle and then the rest of the team review, finalise and then publish each Friday. Away from the office he enjoys cooking and to travel.
Related blogs