Introducing symbolic forms of equations for GCSE Physics and Combined Science
19 July 2022
Ally Davies, Science Subject Advisor

Current GCSE Physics and Combined Science specifications require students to be able to complete physics calculations using specified equations. Feedback from teachers indicated that it would be helpful for us to:
- add to our specifications a list of symbolic equations matching the word equations
- tabulate the chosen symbols, to minimise any confusion and to highlight where confusion might occur.
In this blog I’ve outlined our choice of quantity symbols and the typographical conventions we follow. I’ve explained our use of subscripts, the multiplication symbol and the delta symbol. I’ve included a section on energy, and justified the inclusion of three Greek symbols. I’ve also included links to free helpful classroom resources.
Why symbolic equations?
A tiny proportion of teachers said they preferred not to use symbolic equations, but overall feedback from teachers was very strongly supportive of us introducing symbolic equations.
“Having both symbols and words allows students to recognise the meaning of the symbols but then allows easier mathematical manipulation for questions that require rearrangement.”
“The teaching of symbols forms part of my everyday lessons.”
The barrier to the use of symbols is low for many students (symbolic forms including products, fractions and powers are studied within KS3 maths). However, we understand that not all learners will prefer symbolic forms.
Teachers and candidates should be aware that examiners will not mark with any preference for either symbolic or word forms.
Whilst we are providing a list of our chosen symbols, candidates are free to use word equations or any (clearly defined) appropriate symbols in their answers.
Choice of symbols
Our guiding principles throughout have been accessibility, consistency and clarity.
For some quantities, there is one obvious symbol, e.g. t for time and m for mass. However, there are plenty of quantities for which several symbols are commonly used: for example, x and e are both widely used at this level for ‘extension’ of a spring.
We consulted respected reference sources, including:
- Signs, symbols and systematics (ASE, 2000)
- The language of mathematics in science (LOMIS) (ASE, 2016)
- Teaching secondary physics (ASE, 3rd edition, 2021)
We listened to the views of teachers, assessors and colleagues with expertise in accessibility standards. Where appropriate, we have also sought to align our choices with our A Level specifications.
List of chosen symbols
Teachers told us they need “a key on what the symbols represent”. Each specification already included a list of quantities used within the specification, alongside its designated SI (or SI accepted) unit, and the standard unit abbreviation.
In the revised specification, we have added our chosen symbol for each quantity to this table. Versions of this list are available as a classroom resource. If you are interested to hear more about why we chose each symbol, please do comment below this post.
Typographical conventions – fractions and division, font, spaces, subscripts
Fractions and division
We show division in word equations and in symbol equations consistently through the use of the horizontal fraction bar as shown below. We will not use ÷ or / in either form of equation.
For consistency, we will no longer use ½ or 0.5 to represent ‘half’. Whilst some teachers expressed a preference for 0.5, others made the point that 0.5 might be considered to be an approximate number (containing only one significant figure), when the half is exact in these calculations of kinetic energy and energy associated with a stretched spring.
Font
We use a choice of font for symbols to avoid ambiguity: to avoid possible confusion between the number 1, the lower case letter l (say for length) and the upper case letter I (for current). Italic text is used for quantity symbols and upright text for units, as summarised below.
|
Convention |
Example |
Quantity symbols
|
italic text
|
m for mass, T for time period |
Prefixes and units
|
upright text
|
m for metre, mT for millitesla
|
Spaces
To make symbol equations easy to read, we use a space between quantities when they are multiplied; we use no space between the delta symbol and its relevant quantity. We follow standard conventions for the use of spaces in units. The table below shows these conventions with some examples:
|
Convention |
Example |
Unit abbreviations are multiplied
|
Half letter space between the units
|
N m
|
newton metre
|
for moment of a force
|
Unit abbreviations include a slash (solidus)
|
Half letter spaces around the slash (solidus)
|
N / m
|
newton per metre |
for spring constant
|
Unit with a prefix
|
No space between the prefix and unit
|
nm |
nanometre |
for small length
|
Quantities multiplied
|
Space between quantities
|
I R
|
current x resistance
|
Change (increase) in a quantity
|
No space between Δ and symbol
|
ΔE |
change in thermal/internal energy
|
Subscripts
Teachers and examiners asked for subscripts “only where necessary”. We have included them only in the equations describing the behaviour of an ideal transformer:
In combined science and physics specifications:
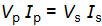
In physics specifications only, and higher tier only:
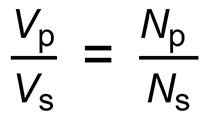
Nonetheless, many teachers spoke of the benefits of subscripts in certain situations, for example indicating before and after a change of pressure and volume (in an ideal gas calculation). Some other possible uses are shown below.
| Quantity |
Example |
To show |
| momentum |
pA pB |
momentum of objects A and B |
| energy |
Ek Eg |
different energy stores, for example kinetic and gravitational |
| material properties |
ρCu ρAl
CFe Cwater
|
comparison of properties of different materials, e.g. density of copper and aluminium |
| moments |
Mcw Macw |
clockwise and anticlockwise moments about a pivot |
If you (and your students) wish to use subscripts, feel free to add them wherever they help.
Multiplication symbol ×
Many teachers expressed a preference for including the multiplication symbol in symbol equations (as well as in word equations). However, we have followed the advice of LOMIS (ASE, 2016), cautioning that multiplication symbols can be confused with an x.
In word equations, we use the multiplication symbol; in symbolic equations, we omit multiplication symbols. An example is shown below.
force exerted by a spring = spring constant × extension
F = k x but not F = k × x
Delta Δ
Delta is used before a quantity symbol to indicate a change in that quantity (strictly speaking an increase in that quantity). For example, ΔE represents a change (increase) in energy.
Most teachers told us that delta would be familiar to their students but we have used it sparingly:
- change in temperature (in degrees Celsius) – Δθ
- change in internal or thermal energy – ΔE
- change in momentum – Δp (change of momentum appears only in B specifications, J259, J260)
To help learners to see the delta as attached to the quantity, we use no space between the delta and the quantity.
All measurements of ‘time’ in GCSE formulas are time intervals or durations, and we have chosen, for simplicity, to use t rather than Δt for all.
In the formula for gravitational potential energy, we have chosen to use h rather than Δh, as our specifications refer to raising an object “above ground level”.
Energy
We have chosen to use E as the subject for all energy calculations; for mechanical work we have used W.
Whilst the use of the initialisms KE, EPE, PE or GPE may be common shorthand in the classroom, many teachers and examiners expressed concern that these may be confusing as the subject of a symbol equation. In contrast with initialisms, by convention, symbols are single letters. For example, PE might be written to mean ‘potential energy’, but could be understood to mean ‘power × energy’.
We have also considered the possible use of subscripts, but we feel that these are unnecessary in these standard formulas – introductory notes and/or the detail of the specification statements make clear which energy calculation is being described.
As with all subscripts, teachers/learners can easily add them if they would find them useful. Ek is in common usage, and Eg would be fairly readily accepted for gravitational potential energy. We hope that you will appreciate the freedom to add subscripts (or not) as you wish.
Greek symbols
We recognise that Greek symbols will be unfamiliar for most students, so in our specification (and below) we spell out the names of any Greek letters we use. With some rationale, we have chosen these three Greek letters as quantity symbols:
- Lambda λ – wavelength; this is the only symbol commonly used for wavelength.
- Rho ρ – density; some may prefer to use D, but ρ is very widely used.
- Theta θ – temperature (degrees Celsius); conventionally T is used for temperatures on the Kelvin scale, so we have chosen not to use T for Celsius temperatures to avoid confusion between these two terms. In the equations required for GCSE, temperature appears only as a temperature change, so we use Δθ. We appreciate that candidates may prefer T to θ, and that candidates may choose to use T or θ alone (i.e. without the delta symbol) to represent a change in temperature. Any clearly defined symbol can be used to achieve full marks in a calculation.
It may be worth highlighting that current GCSE science/physics specifications already expect students to be able to recognise and use some Greek letters:
- nuclear radiations: alpha α, beta β and gamma γ
- the abbreviation for the ohm (the unit of electric resistance), omega, Ω
- the abbreviated unit prefix micro (10-6), mu, μ
Beyond GCSE science specifications, in maths, learners will use pi, π (indeed calculating the area of a circle is covered in KS3 maths). Theta, θ, is also often used to represent angles in maths (for example, in definitions of the basic trigonometric functions, sine, cosine and tangent).
We are grateful to teachers for their feedback which has helped us to prepare three classroom resources. You may wish to print them as posters and/or as references for each learner to keep in their book.
- Formulas to be learnt – a simple list showing each formula in word and symbolic form, using the symbols and conventions outlined above.
Gateway (A suite)
Twenty First Century Science (B suite)
- Physical quantities – a table of all quantities required by the specification with our chosen symbols, the corresponding unit and its abbreviation (this is based on the version included in each revised specification).
Physics (A) Gateway
Physics (B) Twenty First Century Science
Combined Science (A) Gateway
Combined Science(B) Twenty First Century Science
- Alphabet of physics – highlighting for each letter all the symbols/units/prefixes to highlight the scope for, and head off, possible confusion.
Stay connected
If you have any further questions, you can email us at science@ocr.org.uk, call on 01223 553998 or tweet @OCR_Science. You can also sign up to subject updates to receive information about resources and support.
About the author
After teaching physics and science for over 20 years, Ally provided and managed professional support for teachers (at Isaac Physics and for the Institute of Physics). He joined OCR in November 2021. In his spare time, he enjoys nature and the outdoors, walking, cycling and gardening.