A Level Maths: examiner insight on vectors
09 January 2026
Steven Walker, Maths Subject Advisor
Vectors appear in both Pure Maths and Mechanics at A Level.
Examiners’ reports show that while many students earn partial marks, full marks are often lost due to:
- Confusion over notation
- Misinterpreting direction and magnitude
- Poor presentation of working.
This guide highlights some common pitfalls and suggests practical strategies to help students succeed.
Use of diagrams
Examiners often note that students who draw clear diagrams make fewer mistakes and generally score higher. Without a diagram, students often misinterpret the problem or lose track of direction, leading to incorrect answers.
Q2 H240/02 Maths A 2024
Many of the problems seen on this question would have been avoided with a clear diagram, annotated with the length of the vector and the coordinate points identified.
Examiners’ tips:
- Show all relevant points, lines, and directions
- Use arrows for vector direction
- Label coordinates or vector notation clearly
Classroom idea:
- Take a past paper question and redraw it with a clear diagram. Notice how much easier it is to plan your solution.
Magnitude and direction
Always read vector questions carefully to check if the final result should be quoted as a vector, as a magnitude and direction, or as a length. Examiners report that candidates often do not specify direction clearly, especially when answers require angles or bearings. Issues also arise with confusion between scalar and vector quantities.
Q5 H640/02 Maths B (MEI) 2023
In this question students should spot that they have been asked to find the length and not just stating the vector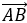 
. A diagram may help as a reminder that the given information is relative to the origin.
A clearly set out solution, explicitly stating the required vector calculation is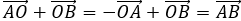 
reduces the risk of sign errors.
Examiners’ tip:
- Re-read the question to make sure you have given the required answer.
Classroom idea:
- Challenge students to create and manipulate vectors using graphing software. This Desmos example uses variables to investigate the vectors given in the question above.
Presentation matters. Examiners highlight that lengthy, unclear working can obscure correct reasoning. To improve:
- Structure your solution logically, step by step.
- Use vector notation consistently.
- Avoid unnecessary repetition – focus on the reasoning behind each calculation.
Q2 H230/01 Maths A 2023
The intended solution route was for clear vector calculations and identifying a simple multiplicative relationship (although converting to points on a linear equations was equally valid). Regardless of method, an initial diagram helps plan the response.
Examiners’ tip:
- Clear working not only helps examiners award marks but also reduces the risk of introducing errors.
Classroom idea:
- Encourage students to peer mark each other’s work.
Issues when using vectors in mechanics
In pure maths, the standard cartesian grid and axis allow a universal definition of a zero point (positive x axis) and direction of turn (anticlockwise). In a real-life situation, the physical constraints mean that a zero point and the direction of turn need to be explicitly defined when giving answers. For example, a force acting on an object held stationary on an inclined plane may be defined as acting on a point at an angle measured below the horizontal. On the other hand, the mathematics that needs to be done remains the same.
Q2 H630/01 Maths B (MEI) 2024
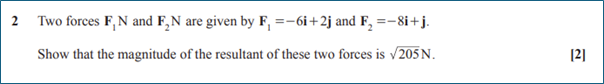
Those students that used a diagram to represent these vectors as either a parallelogram or on a coordinate grid generally identified the resultant vector correctly.
Some students missed out on the final mark by missing out the final step of the magnitude calculation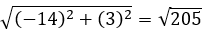 
, and just stating the sum of the squares equal to 205.
Q10 H240/03 Maths A 2023
Set in the mechanics section, the vectors aspect of this question is solved first before applying Newton’s laws.
Examiners’ tip:
- Students who used diagrams – parallelograms or cartesian grid – identified resultant vectors correctly.
Final thoughts
Mastering vectors isn’t about memorising formulas – it’s about visualising problems and presenting your work clearly.
Draw diagrams, check what’s being asked, and keep your working neat. These habits turn partial marks into full marks.
Stay connected
Sign up for our A Level teacher networks each half term and our professional development webinars.
If you have any questions, you can email us at maths@ocr.org.uk, call us on 01223 553998 or message us on social media.
Sign up for subject emails to receive the latest maths news, updates and resources.
If you are considering teaching any of our qualifications, use our online form to let us know, so that we can help you with more information.
About the author
Steven originally studied engineering before completing a PGCE in secondary mathematics. He has taught secondary maths in England and overseas. Steven joined Cambridge OCR in 2014 and worked on the redevelopment of the FSMQ and the A Level Mathematics suite of qualifications. Away from the office he enjoys cooking and to travel. You can follow Steven on BlueSky or Linkedin.
Related blogs