A Level Maths: Binomial expansion in pure and applied maths
21 February 2022
Steven Walker, Maths Subject Advisor
The binomial expansion of (a + b)n is essentially focused on n = 2 at GCSE and then developed further in subsequent Level 3 maths qualifications (FSMQ: Additional Maths – 6993, Mathematics A – H230/H240 and Mathematics B (MEI) – H630/H640), initially for positive integer powers of n, and then for any rational value of n.
Here I look at some of the common mistakes and misconceptions seen by examiners in student responses. I’ll also look at the applications of binomial expansion that could form the basis of Level 3 problem solving and modelling questions.
When n is a positive integer
The FSMQ and AS qualifications limit binomial expansion questions to positive integer powers of n.
Included on the formulae sheet for each is:
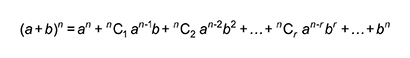
for use when n is a positive integer.
The most common errors with this type of expansion are when there are multiples or negatives involved.
Find the binomial expansion of (1 − 5x)4,
expressing the terms as simply as possible.
Question 6 Core 1 – 4751 June 2016 MEI Mathematics 3895/7895
Whilst this question was done well in most cases, it was not unusual to see
1 – 20x + 30x2… (forgetting to include the multiplying coefficient with each term) or to see
1 – 20x – 150x2… (forgetting to include the negative sign with the indices).
Careful presentation can help avoid these common mistakes. In the classroom I would suggest students set out their work in a column format:
4C0 14 (– 5x)0
4C1 13 (– 5x)1
4C2 12 (– 5x)2
4C3 11 (– 5x)3
4C4 10 (– 5x)4
The terms can then be evaluated before writing out the single result of 1 – 20x + 150x2 – 500x3 +625x4. There is less risk of missing terms, mixing indices or not applying the index correctly to both the sign and coefficient.
This technique may also be useful in questions only requiring the coefficient of a specific term.
Find the constant term in the expansion of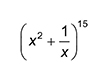 
Question 6 H640/03 June 2018 Mathematics B(MEI) – H640
Students were generally successful here, but those writing out the full expansion would waste valuable exam time
Problem solving in pure maths
Questions where an unknown is included within a binomial expression are an example of problem solving.
It is given that, in the expansion of (3 + kx)3, the coefficient of x2 is equal to the constant term.
Find the possible values of k, giving your answers in an exact form.
Question 3 Core 2 – 4722 June 2016 OCR Mathematics 3890/7890 (edited)
Again, setting the response out in a column format allows students to identify the appropriate terms before any calculations are needed.
3C0 33 (kx)0
3C1 32 (kx)1
3C2 31 (kx)2
3C3 30 (kx)3
A common mistake on this question was assuming k > 0. Many students reached 27 = 9k2 but, having found k = √3, didn’t include k = – √3.
Modelling accurate calculations
One application of binomial expansion is to determine exact results for calculations that would not be possible using a calculator.
For example, the exact result of the calculation (0.0103)5 can be found using a binomial expansion such as (1 × 10-2)5 (1 + 3x)5 with x = 0.01.
The expansion of (1 + 3x)5
5C0 15 (3x)0
5C1 14 (3x)1
5C2 13 (3x)2
5C3 12 (3x)3
5C4 11 (3x)4
5C5 10 (3x)5
= 1 × 10–10 (1 + 5(3x) + 10(3x)2 + 10(3x)3 + 5(3x)4 + (3x)5)
= 1 × 10–10 (1 + 15(0.01) + 90(0.01)2 + 270(0.01)3 + 405(0.01)4 + 243(0.01)5)
= 1.152 704 074 3 × 10–10
Other substitutions are valid, but students should ensure that the working is clear and they have confidence that the individual terms can be evaluated exactly.
For example, (0.0103)5 could be written as (1×10-2)5 (1 + x)5 where x = 0.03. However, the alternative form (1 × 10-4)5 (2 + x), with x = 101, would be problematic, since a standard calculator could only display an approximate solution for 1015 ≈ 1.05101005 × 1010.
There is no restriction on the values of a or b in the expression (a + b). However, it is not unusual to expect the values to be limited to 1 significant figure in order to allow confidence with the numerical terms when evaluating exact results. Making either a or b equal to 1 also helps simplify the arithmetic.
Binomial distribution model
Binomial expansion is important in binary outcome experiments. Here, the expression used is often written as (p + q)n where p is the probability of a successful outcome, n is the number of attempts and q = 1 – p.
In a factory, an inspector checks a random sample of 30 mugs from a large batch and notes the number, X, which are defective.
If X > 2, the batch is rejected. It is given that 5% of mugs are defective.
Find the probability that the batch is rejected after just the first sample is checked.
Question 7 Probability and Statistics 1 – 4732 Jun 2013 OCR Mathematics 3890/7890 (edited)
When this question was set in 2013, students were expected to use statistical tables rather than using the expansion formula, whereas now the expectation is that students use the binomial distribution function on the calculator. For some students however, the written expansion will help avoid the common confusion between P(X = 2), P(X ≤ 2) and P(X ≥ 3). Using p = 0.95 or p = 0.05 is equally valid, but a sketched distribution curve may help avoid introducing further confusion in solutions.
The synoptic nature of the current A Level Maths means that the link between binomial expansion and binomial distributions may be more explicit.
- Write down and simplify the first four terms in the expansion of (x + y)7. Give your answer in ascending powers of x.
- Given that the terms in x2y5 and x3y4 in this expansion are equal, find the value of
.
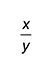- A hospital consultant has seven appointments every day. The number of these appointments which start late on a randomly chosen day is denoted by L. The variable L is modelled by the distribution B (7,
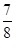). Show that, in this model, the hospital consultant is equally likely to have two appointments start late or three appointments start late.
Question 10 H230/01 SAM AS Mathematics A – H230
General expansion
In A Level Maths, the topic progresses to include fractional and/or negative indices. The A Level Maths formulae sheet includes
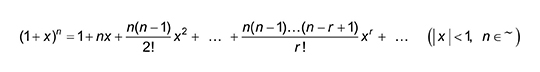
Use the expansion (1 + 3x)0.5 to find an estimate for √103, correct to five decimal places.
Question 2 H240/02 June 2019 Mathematics A – H240 (edited)
A common mistake on this question was to attempt x = 34, ignoring the constraint that |x|<1. Successful students generally spotted that 103 = 100 × 1.03 and so used √103 = 10 (1 + 3x)0.5 where x = 0.01.
Applications in calculus
A particularly useful application of binomial expansion is in finding approximations for complex functions, which can then be easier to differentiate or integrate.
Find the binomial expansion of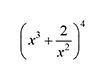
and hence find
.
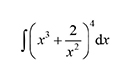Question 6 Core 2 – 4722 June 2014 OCR Mathematics 3890/7890 (edited)
Students generally avoided careless mistakes as long as they used brackets around each part of the binomial product and remembered to include the nCr component. A few did however express terms such as (x3)4 incorrectly as x7, or mistakenly evaluated terms such as
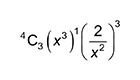as 32 x3.
With the expression successfully expanded, students generally found the subsequent integration relatively straight forward (though arithmetic mistakes were seen with negative indices and the perennial omission of ‘+ c’).
Support
For further past paper feedback, see the examiner reports on the ‘Assessment’ area of our qualifications’ webpages (A Level Maths A – H240 and A Level Maths B (MEI) – H640), where you can also find the papers themselves. (Papers for autumn 2021 are currently held on Interchange). Further questions can be found in the legacy papers available on ExamBuilder, our free question-building platform.
You can find resources such as delivery guides and section check in tests in the ‘Planning and teaching’ area for each qualification.
A set of introductory videos and exercises for this topic are available on the binomial theorem section on the Khan Academy site.
For a nice challenge, try the numerical problem in the section on counting and binomials on Underground Maths.
Stay connected
There are many great online resources available, so join the conversation by sharing your ideas and links to all your favourites in the comment box below.
If you have any queries you can email us at maths@ocr.org.uk, call us on 01223 553998 or tweet us @OCR_Maths. You can also sign up for monthly email updates to receive information about resources and support.
About the author
Steven Walker, OCR Maths Subject Advisor
Steven joined OCR in 2014 during the major qualification reform period and now primarily focuses on supporting the Level 3 maths qualifications. He originally studied engineering and then took an extended period to work and travel around the world before completing a PGCE in secondary mathematics. Steven began his teaching career with VSO in Malawi and has taught maths in both the UK and overseas.
Related blogs