A Level Maths: Trigonometry, not just for triangles – part 2
12 May 2021
Hints and tips - 5 minute read
 Steven Walker, Maths Subject Advisor
Steven Walker, Maths Subject Advisor
Part 1 of this blog is available to read here.
Trigonometry is introduced as a technique to solve geometric problems focused on triangles at GCSE, but at A Level the link between geometry and the given equations can be lost. This topic can be challenging for many students, but the use of dynamic geometry can help understanding through visualisation. Here I look at some of the common misconceptions seen by examiners and discuss ideas for supporting students’ understanding.
Inverse and reciprocal functions
In standard algebra (the reciprocal function)
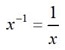 but
but 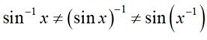
Examiners note some confusion seen when students are handling the inverse function and also when switching between the standard functions and the reciprocal trig functions (secant, cosecant and cotangent). For a quick demonstration of the notation it may be worth looking at the different graphs (see Reciprocal or inverse Desmos graph).
Other notation issues
Students can confuse themselves by mixing multiples and indices, for example writing cos2 θ when they mean cos2θ, or vice versa. Similarly, examiners sometimes report seeing misconceptions between y=sin2 x and y=sin (x2). Again students may benefit from looking at the different families of graphs for each function (see Index sine Desmos graph).
Pythagoras identities
The link between the algebra involved in trigonometry and physical geometry is often overlooked. A nice introduction to the topic of identities is for students to refer back to the standard right-angled triangle and manipulating Pythagoras’ theorem.
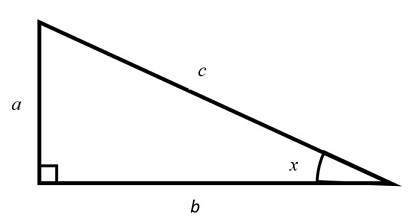
Students need to be comfortable with general algebraic manipulation, but would also benefit for seeing graphically what these represent.
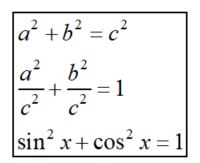
Examiners have noted that a few students mistakenly believe that it is simply the sum of sine and cosine, rather than the sum of the squares, that equals one (for a quick demonstration of the relationship see trig identity 1 on Desmos).
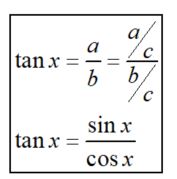
Some students seem to forget the relationship between sine, cosine and tangent. A visual representation (such as trig identity 2 on Desmos) may help.
Transformations
Common errors in questions comparing y = f(x) with y = af(x + b) + c involve students recognising the transformation, but giving their answer in the opposite sense, such as translating upwards rather than downwards, left rather than right, or scaled up rather than down.
Marks may also be dropped when the order of a sequence of transformations is quoted incorrectly, such as stating a stretch before a translation rather than a translation followed by the stretch.
Dynamic geometry is a useful tool to investigate transformations. Students can quickly see how object and image change as the order of transformation is switched (see this transformations of sine curve example on Desmos).
Compound angle formulae
Standard compound angle identities such as sin (x + a) are given in the formulae sheet, yet students are expected to be able to follow a geometric proof for these (see compound angle in Desmos for a starting point to investigate the relationships).
These compound angle identities lead into the double angle, half angle and multiple angle formulae. Common errors are generally linked to mistakes in the algebraic manipulation.
They also lead into the ‘harmonic’ identities such as Rsin (x + θ) = asin x + bcos x. Most students identify the value for R, but often invert the a/b when finding θ. Solutions obtained by graphical investigation shouldn’t be expected to gain credit in the exam, but may be a good introduction in the classroom (see acosx+bsinx on Desmos).
Those students that communicate each step of the mathematical argument, making clear their use of the Pythagoras Identities in the calculations are generally more successful on questions on this topic.
Hence
Often part (a) of a question will involve students having to prove something (or less formally ‘Show that…’), then part (b) will require that general form be used to solve a specific equation. The command word ‘Hence…’ is often used to explicitly draw attention to the link between the two parts. Students should remember that the part (b) marks here will be available to them, even if they did not complete part (a).
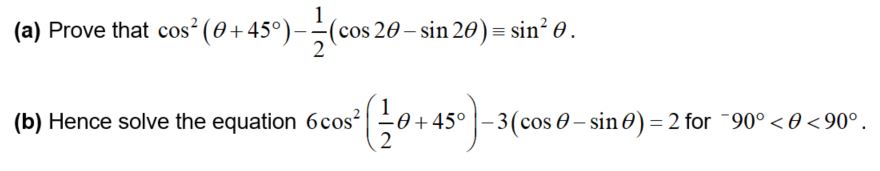
Q9 Core 3 4723 Mathematics 7890 Jan 2013 (edited)
Examiners noted that most candidates who attempted part (a) were confident with the expansion of (cos 2θ - sin 2θ), but struggled with cos2 (θ + 45°). However, they were still able to pick up marks in in part (b) by recognising the link between its equation and the identity in part (a).
Support
The links to graphs in this blog may be useful starting points for developing resources. For even more resources, see the trigonometry delivery guide for your qualification (Maths A H240 or Maths B (MEI) H640, or download them from your qualification’s ‘Planning and teaching’ area).
For further exam paper feedback, see the examiner reports and candidate exemplars available from your qualification’s ‘Assessment’ area (Maths A H240 or Maths B (MEI) H640).
Feedback on questions from legacy papers is also available in ExamBuilder, our free question-building platform.
Stay connected
There are so many great online resources available, so join the conversation by sharing your ideas and links to all your favourites in the comment box below.
If you have any questions, email us at maths@ocr.org.uk, call us on 01223 553998 or tweet us @OCR_Maths. You can also sign up for email updates to receive information about resources and support.
About the author
Steven joined OCR in 2014 during the major qualification reform period and now primarily focuses on supporting the Level 3 maths qualifications. Steven originally studied engineering before completing a PGCE in secondary mathematics. He began his teaching career with VSO in Malawi and has taught maths in both the UK and overseas.
By the same author