A Level Maths: Trigonometry, not just for triangles – part 1
27 April 2021
Hints and tips - 7 minute read
Steven Walker, Maths Subject Advisor
Trigonometry is used at GCSE as part of geometry and mensuration, primarily focused on triangles, but with an introduction to functions and graphs. At A Level, students use these skills to solve problems in the mechanics strand and also look at how the cyclic nature of these functions can be used in complex algebraic and calculus problems. This initial blog looks at some of the mistakes commonly seen by examiners.
Sine cosine confusion
SOHCAHTOA is the mnemonic many students memorise to good effect at GCSE to solve problems involving right-angled triangles. However, this only helps if the sides and angles are identified correctly. One area of A Level Maths where right-angled triangles are used regularly is in mechanics problems involving objects on slopes, either in equilibrium or moving up or down the slope.
A force P N is applied to the block parallel to the plane in the upwards direction.
The plane is rough so that a frictional force of 10 N opposes the motion.
The block is moving at constant speed up the plane.
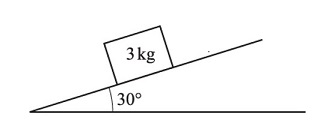
Q1 Mechanics 1 4761 January 2013 Mathematics MEI (edited)
Most candidates recognise that the force due to gravity needs to be resolved parallel and perpendicular to the slope, but problems are often seen with confusion between the use of sine and cosine. A separate right angled triangle may help avoid this confusion.
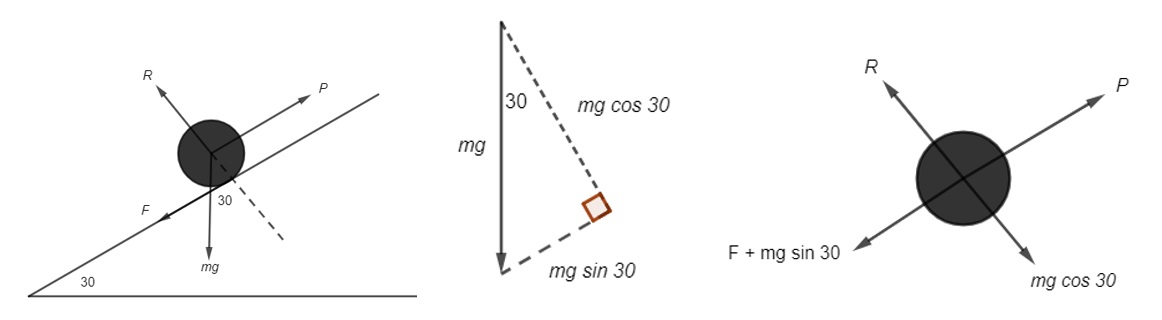
Mark schemes often allow method marks if it is clear that the only mistake is with a sin/cos confusion. However, correct answers obtained from wrong working (for example with a slope inclined at 45º) will be penalised.
Exact values
One of the new specification items on the GCSE (9–1) Maths content is knowing specific exact values of sin θ, cos θ and tan θ for stated values in the range 0º-90º, which extends at AS Level to stated angles up to 180º along with multiples of them. Candidates are advised to use the exact values (rather than decimal approximations) where possible and it is common for mechanics problems to involve 30º, 45º or 60º angles to facilitate this. Alternatively, problems may give the exact value of the sine of the slope angle as a fraction.
The train now comes to a place where the track goes up a straight, uniform slope at an angle α with the horizontal, where:
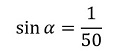
Q7 Mechanics 1 4761 June 2012 Mathematics MEI (edited)
Here it is expected that candidates use the Pythagoras identity to state the cosine of the angle rather than calculating the angle first.
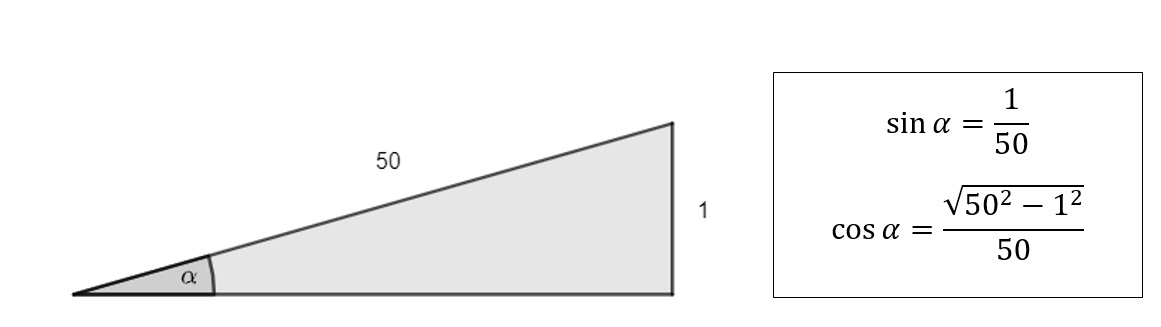
Often the numbers have been chosen to provide nice cancelling, which means candidates finding a decimal approximation may risk introducing errors or just having more work to do.
Introducing radians
GCSE and AS Maths only use degrees, but at A Level (and AS Further) radians are introduced.
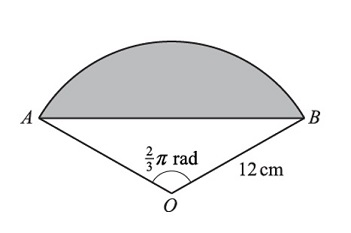
Students first use radians to solve sector and segment problems.
The diagram shows a sector OAB of a circle, centre O and radius 12 cm.
The angle AOB is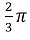 
radians.
Q3 Core 2 4722 June 2014 Mathematics (edited)
Examiners often note that candidates waste time converting radians into degrees rather than working with the given units.
This also links into the second problem noted by examiners: marks being dropped where candidates forget to switch calculator mode from degrees to radians (and back again) as appropriate for the set questions (for general calculator advice see Will Hornby’s blog The truth about calculators for Maths A levels).
Degrees or radians?
Method marks will generally be available if clear working is shown but the accuracy marks will not be awarded if the incorrect angle units are used.
Questions requiring trigonometric equations to be solved will explicitly state if the question is in degrees or radians (see my earlier blog for general comments on solving trigonometrical equations that rearrange into a quadratic format).
Graphs and calculus questions involving trigonometric functions are always performed using radians. The reason for this is not explicitly covered in A Level Maths, but are linked to 360 degrees being an arbitrary unit of measurement for a full rotation (read about the historic background) whereas 2π radians is a natural measurement for a full rotation regardless of the radius. For example, in radians ∫cos x dx = sin x + c, but working in degrees would involve an additional multiplying factor. Trigonometric functions plotted alongside their inverse functions would also look strange in degrees (see trig inverse desmos graph).
The advanced algebra covered in Further Maths, such as complex numbers, hyperbolic functions and the Maclaurin expansions are all in radians (similarly, the small angle approximations are quoted for radians in A Level Maths).
Mechanics questions generally involve degrees when investigating linear motion (A Level Maths), but radians when investigating circular motion or the centre of mass of circular objects (Further Maths).
Support
For delivery guides and check–in tests for our two specifications (H240 and H640), see below:
For an interactive review of resolving forces on a slope try the Geogebra activity by Amy Scudder. For a quick quiz review of trigonometry in radians try the unit circle (with radians) activity from Khan Academy.
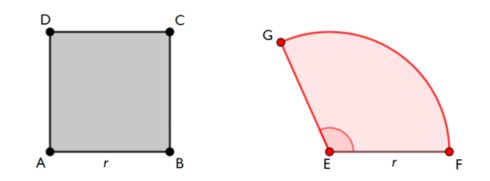
Also keep an eye out for our Friday puzzles Tweeted using #OCRmathspuzzles. Here's an example from 11 September 2020. Compare the working needed to find the angle in degrees or the angle in radians.
Square ABCD has side length r.
Sector GEF is a sector of a circle with radius r.
Square ABCD and sector GEF have the same perimeter.
What is the exact size of angle GEF?
Continue on to part 2 of this blog.
Stay connected
There are so many great online resources available, so join the conversation by sharing your ideas and links to all your favourites in the comment box below.
If you have any questions, email us at maths@ocr.org.uk, call us on 01223 553998 or tweet us @OCR_Maths. You can also sign up for email updates to receive information about resources and support.
About the author
Steven joined OCR in 2014 during the major qualification reform period and now primarily focuses on supporting the Level 3 maths qualifications. Steven originally studied engineering before completing a PGCE in secondary mathematics. He began his teaching career with VSO in Malawi and has taught maths in both the UK and overseas. He is currently balancing his ‘work from home’ commitments with supporting his daughter with her year one lessons.
By the same author