A Level Maths: Using graphs to investigate quadratic functions
25 January 2021
Hints and tips - 7 minute read
 Steven Walker, OCR Maths Subject Advisor
Steven Walker, OCR Maths Subject Advisor
Following on from my previous blogs discussing support for students working remotely, here I turn my attention to quadratic functions.
In this blog I will highlight some of the examiners’ feedback from questions on this topic and look at the use of graphing software to reinforce learning.
The links between quadratic graphs and equations is one of the fundamental of A Level Maths. Although the topic is introduced in Key Stage 3, at A Level an in-depth knowledge is required to tackle problems set.
Note that the question examples I have used are all from the legacy qualifications. This was deliberate to highlight that the issues are not simply a result of the qualification reform.
Command words and the use of calculators
For the current A Level Maths qualification, students should be confident in using their calculator for any function it can perform.
The command word used in each question will indicate whether candidates can just write down the answer from their calculator screen, or if their response needs to include clear mathematical steps working towards the answer.
For example, questions asking candidates to ‘Show that…’, ‘Determine…’ or the bold statement ‘In this question you must show detailed reasoning’ there must be sufficient written working to demonstrate an understanding of the mathematics.
Full definitions of the Command words that will be used in A Level Maths A and Maths B (MEI) are given in the qualifications’ specifications. We’ve also produced useful command word posters. For even more exam hints, see our guides for Spec A and Spec B as well as our calculator use poster.
Linking the graph with the algebra
Candidates often start manipulating the algebra in an equation without fully thinking about what they are trying to achieve. Graphical visualisation can help to plan a solution.
For example, question 2 from Core 1 (4721), June 2017:
Solve the simultaneous equations y = x2 – 6x and 2y + x – 6 = 0
The standard approach to this type of question is to eliminate one variable and then solving their subsequent quadratic equation. However, a recurring mistake is for candidates to stop with a value for x or for y, but not finding solutions as coordinates (x , y)
Candidates should recognise this pair of equations will give a U shaped parabola and a downward sloped line and that there could be 2 solutions (line crosses curve twice), 1 solution (tangent) or no solutions (line does not cut the curve).
Create new questions by changing the coefficients (try this ‘Intersecting quad with linear’ demonstration written on Desmos).
Completing the square
Students will be familiar with solving quadratic equations, plotting quadratic graphs and finding turning points of a quadratic function from Higher tier GCSE. However, these are often taken as distinct techniques rather than as a set of linked tools for curve sketching. These links may even become further disconnected once calculus is introduced to identify turning points.
The usefulness is not always recognised of a quadratic equation written in the completed square format, i.e. a(x + d)2 + e.
For example, question 4 from Core 1 (4721), June 2017:
Sketch the curve y = – 0.5 (x + 1)2 + 2 giving the coordinates of the turning point and indicating all points of intersection with the axes.
It is common to see candidates obtaining the three term quadratic equation by multiplying out the brackets, then differentiating to find the turning point and factorising to find the x–intercepts (stating the y–intercept as y = 2 is also a common mistake).
A useful activity to challenge students is matching quadratic equations in the three term format with their completed square format. This can be done using dynamic graphing software, such as this ‘equivalence graphing sheet’ demonstration on Desmos.
Developing fluency in switching between the two formats will be an advantage when moving onto transformations of graphs. The completed square format makes it easy to compare transformations of quadratic functions. Another activity that can be useful is this ‘Transformation of x squared’ demonstration.
Inequalities
Another related topic is inequalities.
For example, question 4 from Core 1 (4751), Jan 2013:
Solve the inequality 5x2 – 28x – 12 ≤ 0
Candidates often struggle with identifying the direction of the inequalities in the final answer. Again, a sketch would help candidates recognise if the solution set should be the region of the graph above or below the x-axis.
Take a look at this ‘Inequalities’ resource on Desmos.
Algebraic manipulation
Many strong mathematicians still lose accuracy marks through arithmetical errors. This includes things such as adding rather than multiplying, multiplying by n rather than raising to index n and missing out brackets. For further support, see our Bridging the Gap resource for students starting year 12.
OCR Support
For a range of exam questions, see the practice and past papers on the Mathematics A H230/H240 and Mathematics B (MEI) H630/H640 qualification webpages, as well as Interchange. For notes on common mistakes and misconceptions see the examiners’ reports.
ExamBuilder is a useful tool for quickly sourcing specific topic questions. Use the filters to locate all the appropriate questions along with the respective mark schemes and examiners’ report comments.
Questions from legacy qualifications can be used with current students, but they may need to be adapted so that they’re in line with the current command word usage. For support in adapting legacy questions, see our ExamBuilder guide.
The following Check In tests and Delivery guides will be useful on this topic. For the full range of these resources, see the ‘Planning and teaching’ section of the qualification pages.
This topic overlaps with the algebra and graphs content in GCSE, see our GCSE (9 – 1) Mathematics – J560 Higher Tier Check in Tests for a recap (Section 6 and section 7).
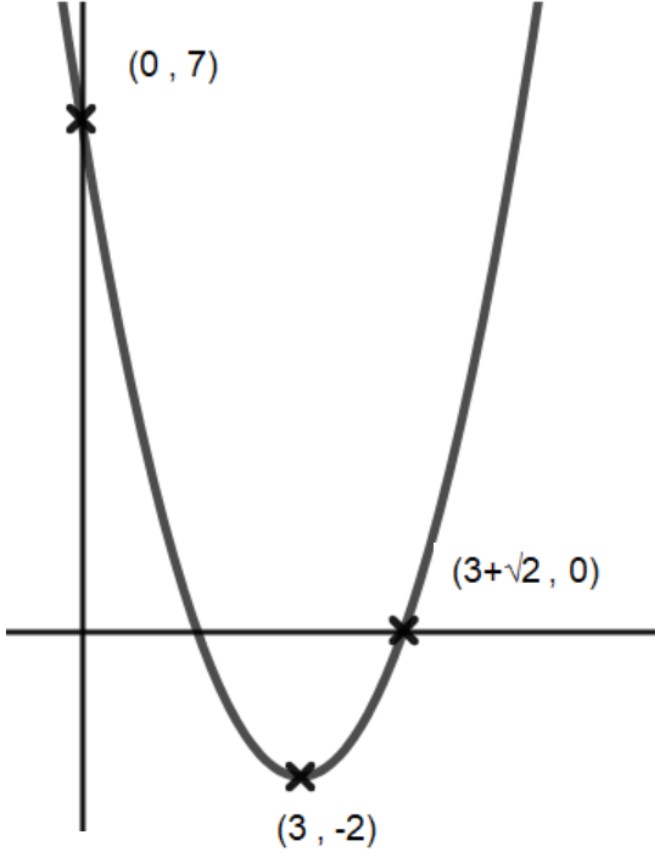
You may also enjoy our Friday maths puzzles posted on @OCR_Maths using #OCRmathsPuzzle. Below is an example featuring the graph of a quadratic function.
What is the equation of the quadratic graph that passes through the points (0,7), (3, -2) and (3+√2,0)?
Stay connected
There are so many great online resources available, so join the conversation by sharing your ideas and links to all your favourites in the comment box below.
If you have any questions, email us at maths@ocr.org.uk, call us on 01223 553998 or Tweet us @OCR_Maths. You can also sign up for monthly email updates to receive the latest information about resources and support.
About the author
Steven Walker, OCR Maths Subject Advisor
Steven joined OCR in 2014 during the major qualification reform period and now primarily focuses on supporting the Level 3 maths qualifications. Steven originally studied engineering before completing a PGCE in secondary mathematics. He began his teaching career with VSO in Malawi and has taught maths in both the UK and overseas. He is currently balancing his ‘work from home’ commitments with supporting his daughter with her year one lessons.
By the same author